Recursion in C

Recursion

Recursion and Iteration are two different concepts of achieving a result by a number of repeated operations. Iteration involves use of for, while and do-while loops for the repeated operation until specified condition. Recursion involves a recursive function calling itself several times until specified condition.

A recursive function represents the most simpler form of a complex task. Suppose the complex task can be divided into ‘n’ simple tasks. Now after ‘n’ recursive operations involving the same recursive function, the result is obtained. Recursion could also be invoked by recursive chains in which more than one function calls each other.

Now, a recursive definition or algorithm could be defined as a simpler version of a complex task. This simpler case is repeated several times until the required result is obtained at specified condition. While writing a recursive definition, we should make sure that the recursive calls will terminate after specified operation. Otherwise, it will result in a non-terminating sequence of calls or an infinite loop.

Consider a factorial function n!. We could divide n! into simpler cases of itself and thus  generate a recursive definition as follows –

n! = n(n-1)! = n(n-1)(n-2)! = n(n-1)(n-2)!(n-3)!

Thus, the recursive definition is,

n! = 1 if n = 0
n! = n*(n-1)! if n > 0

The recursive algorithm for the function fact() could be –

if(n == 0)
   return(1);
else
    return(n*fact(n-1));

Thus the recursive routine for factorial function could be –

int fact(int n)
{ return ( n==0 ? 1 : n*(fact(n-1))); }

Below are sample recursive functions in C –

1) Factorial

Recursive definition

n! = 1 if n = 0

n! = n(n-1)! = n(n-1)(n-2)! = n(n-1)(n-2)!(n-3)!

Recursive algorithm

/*recursive algorithm for fact(n)*/
if(n == 0)
   return(1);
else
    return(n*fact(n-1));

C Program

/*C routine for fact(n)*/
int fact(int n)
{ return ( n==0 ? 1 : n*(fact(n-1))); }

2) Multiplication

Recursive definition

Let a and b be two integers then a x b is recursively defined as,

a x b = a x (b-1) + a = a x (b-2) + a + a etc ..

Recursive algorithm

/*recursive algorithm for mult(a,b)*/
    return(b == 1? a : mult(a,b-1) + a);

C Program

/*C routine for mult(a,b)*/
int mult(int a, intb)
{ return ( b == 1? a : mult(a,b-1) + a); }

3) Fibonacci Series

Recursive definition

fib(n) = 1; if n = 0 or n = 1
fib(n) = fib(n-2) + fib(n-1)

Recursive algorithm

/*recursive algorithm for fib(n)*/
    if(n == 0 || n == 1)
        return(n);
    else
        return (fib(n-2) + fib(n-1));

C Program

/*C routine for fib(n)*/
int fib(int n)
{ 
    if(n == 0 || n == 1)
        return(n);
    else
        return (fib(n-2) + fib(n-1)); 
}

4) Binary Search

Recursive algorithm

/*recursive C program for binsearch()*/
/* a[i] is the sorted global array */
/* n is the number of elements in array */

scanf("%d", &x); /*inputs number to be searched - global*/
low = 0; high = n -1;

int binsearch(int low, int high, in a[], X){

         int mid;
         if(low > high){
            return(-1);
         }
         mid = (low + high) / 2;
         return(X == a[mid] ? mid : X < a [mid] ? binsearch(low, mid-1, a[], X) : binsearch (mid+1,high,a[],X))


}

Recursive Chains

Recursive chains involves two or more than two functions calling each other. The following is the structure of two function calling each other –

a(formal parameters)                                               b(formal parameters)

{                                                                                    {

.          .            .                                                             .          .            .

.          .            .                                                             .          .            .

b(arguments);                                                            a(arguments);

}                                                                                     }

Conditions should be set that the recursive chains do not form an infinite loop.

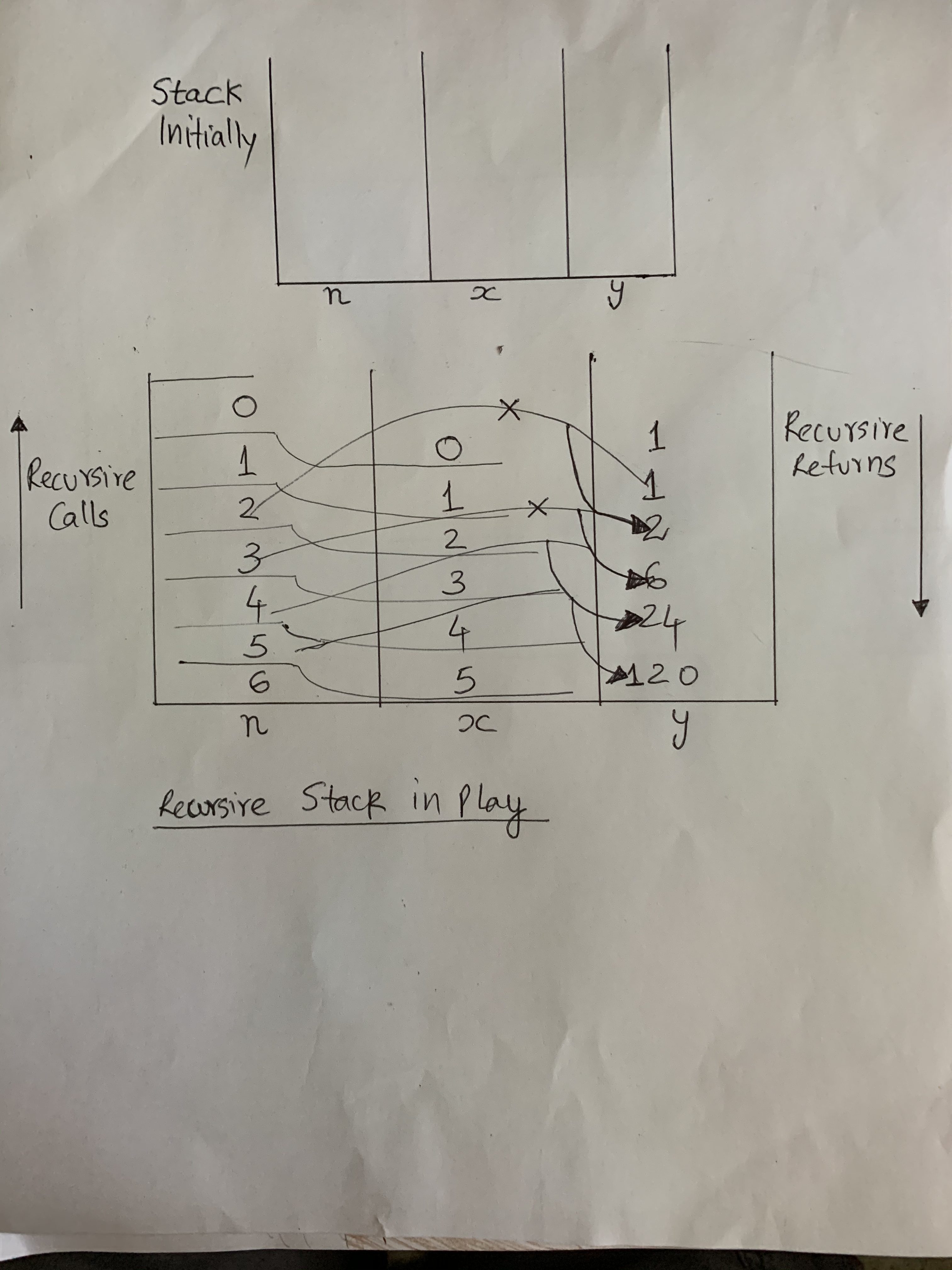
Stacked view of recursive calls

Let us take the example of factorial function and explain the stacked view of recursive calls –

int fact(int n)
{ 
  if(n < 0)
      printf("\nInvalid Input");
  else
      return ( n==0 ? 1 : n*(fact(n-1))); 
}

—– Or —–

int fact(int n)
{ 
  int x, y;
  if(n < 0)
      printf("\nInvalid Input");
  else if(n == 0)
      return (1);
  else{
      x = n - 1;
      y = fact(x);
      return (n*y); 
  }
}

Suppose the call is –

printf("%d", fact(6));

The various stages of recursion could be viewed by using a stack. Every time a recursive call is made, new generations of local variables and parameters are generated and are pushed to a stack as a recursion is entered. Now, as the recursive function returns, each generation of local variables and parameters are referenced by popping the stack till all returns are completed. Below image shows the Recursive Stack in action –