Implementing Ford Fulkerson’s Algorithm in C To Maximize Network Flow

Flow Problem

The main objective of a flow problem is to maximize the amount of an item being delivered from one point of a system to another. If we consider a water pipe system as shown below, our objective would be to maximize the amount of water flowing from source S to sink T.

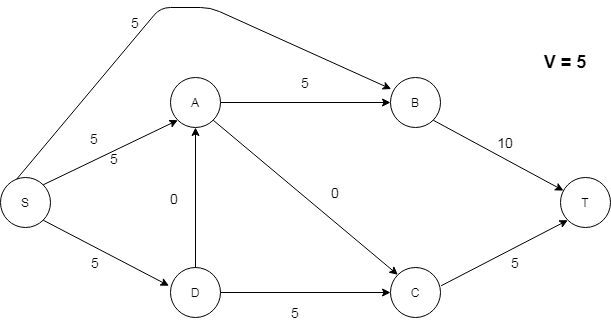
The entire pipe system is represented as a network. Arcs represents pipes and nodes represents connection between pipes. S is the source and T is the sink. The weights of each arcs represents the amount of water flowing. We define a function C(a,b) called capacity function which gives capacity of pipe from a to b, C(a,b) > = 0, if C(a,b) = 0, there is no such pipe from a to b. Another function f(a,b) called the flow function f(a,b) gives the actual amount of water flowing from node a to b such that f(a,b) >= 0 and f(a,b) <- C(a,b). If V is the total amount of water flowing through the system, then for the watr pipe system, the amount of water flowing out from source S must be equal to V which is equal to amount of water flowing into T.

i.e. Σf(s,x) = V =  Σf(x,T) ; where x is an element of node

Also amount of water entering a node other than S and T be equal to the same leave that node. i.e. if we define two terms inflow and outflow,

A perfect FLOW FUNCTION for a water pipe system would be,

i) Outflow(s) = inflow(T) = V

ii) Inflow(x) = outflow(x), for all x != S,T.

So, while designing a better water pipe system our objective would be to improve the various flow functions satisfying the above conditions so that the value of V is maximized.

Methods to improve Flow V

There are generally two methods to improve the flow. They are as follows –

Method 1: 

Consider a  network shown below –

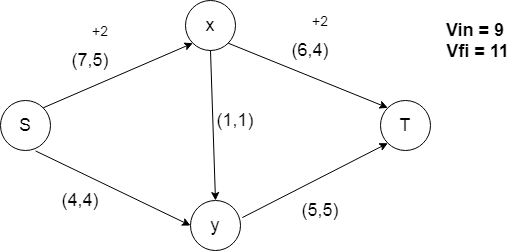
Consider the semi-path {<s, x>, <x,T> }. The flow between nodes S, x could be increased by 2 and this increase could be accommodated by arc <x,T> by a corresponding increase of 2. Thus the flow V could be increased from an initial value of 9 to 11.

Method 2: 

Consider a  network shown below –

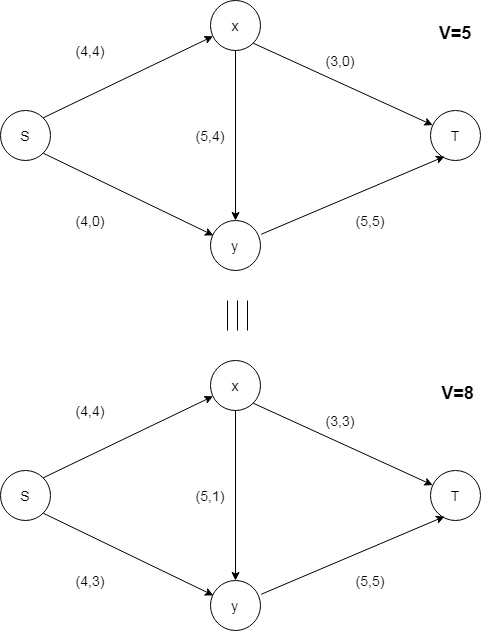
It is seen that the flow along <S,y> and <x,T> could be increased by a value 3 by reducing the flow through the arc <x,y> to a minimum by an amount  = (4-3) = 1. Now, if we are given any pipe network, the above methods could be applied wherever necessary to increase the flow V from S to T.

Ford Fulkerson’s algorithm to maximize the flow V of a network

The algorithm uses the above two methods of maximizing flow functions of arcs this increasing the flow V. Consider the following network which we have to maximize the flow V –

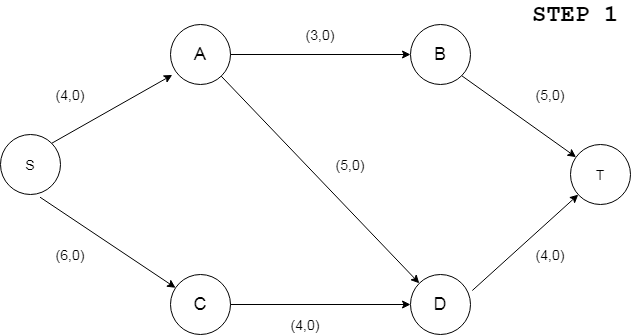
The first step would be to initialize all the flow functions of arcs to 0. Next, we consider all partial semi-paths which form a complete path from S to T for eg: <S A B T>, <S A D T>, <S C D T>. The algorithm finds all these partial semi-paths one by one. Once it finds a partial semi-path i.e. traversing from node S to T through all possible nodes, it them traverses backwards by adjusting the flow functions of each arc associated with that partial semi-path. The process is repeated for all partial semi-paths till the flow is optimal.

Step:1 For the above network as per the algorithm, we have initialized all flow functions to zeroes. Now, as a next step, the algorithm finds a partial semi-path <S A B T> and traverses it from S to T. While starting from S, inflow from S could be increased to a maximum of 4. While traversing back, from T to S, the algorithm adjusts the flows at arcs <B T>, <A B> and <S A> as 3, 3 and 3 respectively since the maximum capacity of <A B> is only 3. The resulting network of Step 2 is as shown below –

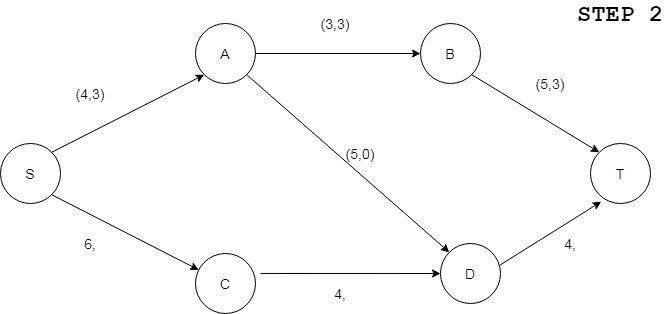
Now the algorithm finds another partial semi-path <S C D T> and repeats the above procedure of adjusting the flows and the resulting network is shown below –

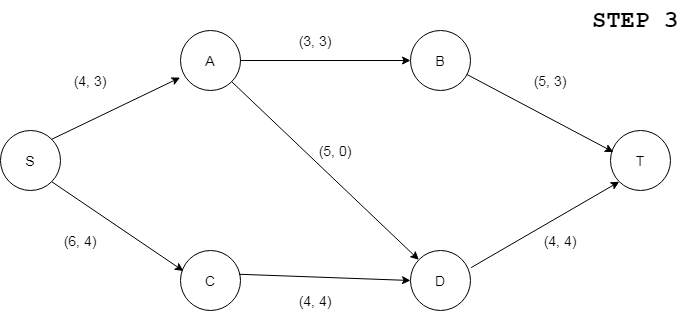
Now since an optimal flow V has reached with V = 7, the algorithm stops at this stage. Ford’s Fulkerson’s algorithm could be written as –

  Initialize all flow functions to 0;
  canimprove = TRUE;
  
  do{
      attempt to find a semi-path from S to T that increases the flow to T by x, x > 0;
      if(no such semi-path){
           canimprove = FALSE;
      }
      else{
           increase the flow-functions in semi-path by x
      }
  }while(canimprove == TRUE);